Symmetrie und Kongruenz

1. Einleitung

Symmetrie lässt sich wohl überall entdecken. Sie fasziniert und ist eine der ganz großen Ideen. Mathematik ist die Wissenschaft, in deren Sprache Symmetrie am klarsten zu fassen ist und mit deren Mitteln ihre Eigenschaften am sichersten zu erschließen sind. Symmetrie ist ein unmittelbar faszinierendes Phänomen und in vielen Lebensbereichen bedeutsam: Lebwesen weisen in hohem Maße Symmetrie auf, die Kunst ist von Symmetrie durchdrungen, technische Geräte sind häufig aus funktionalen Gründen symmetrisch. Symmetrie ist offenbar eine schwer zu überwindene Einschränkung unseres Vorstellungsvermögens selbst da, wo der Phantasie keine Grenzen gesetzt scheinen: Auch fiktive Lebewesen (sogar die Bösen) und Fahrzeuge sind fast ohne Ausnahme bilateral symmetrisch. Der Seitenscheitel ist einer der wenigen mehrheitsfähigen Symmetriebrüche. Der Mathematiker Hermann Weyl schrieb 1955: „Symmetrie, ob man ihre Bedeutung weit oder eng faßt, vermöge derer der Mensch durch die Jahrtausende seiner Geschichte versucht hat, Ordnung, Schönheit und Vollkommenheit zu begreifen und zu schaffen.”

Bildquellen angegeben unter [1], [2] und [3] im sechsten Kapitel unter Bildnachweise.

2. Fachlicher Hintergrund

Es existieren vier verschiedene Abbildungen und Arten der Symmetrie, die im Anschluss zum Begriff der Kongruenz führen.

Achsenspiegelung
- → Achsensymmetrie
Punktspiegelung
- → Punksymmetrie
Drehung
- → Drehsymmetrie
Verschiebung
- → Verschiebungssymmetrie

In den folgenden vier Unterkapiteln werden die einzelnen Abbildungen und Arten definiert und schließlich mit dem Begriff der Kongruenz verbunden.

2.1. Achsenspiegelung & Achsensymmetrie

(2.1) Definition (Achsenspiegelung)

Eine Abbildung \( S_g \) der Ebene auf sich heißt Achsenspiegelung an der Achse \( g \), wenn für alle Punkte \( P \) gilt:

\( S_g(P) = P \) für \( P \in g \)
\( S_g(P) = P \) für \( P \not\in g \) und \( g \) Mittelsenkrechte von \( [PP'] \)

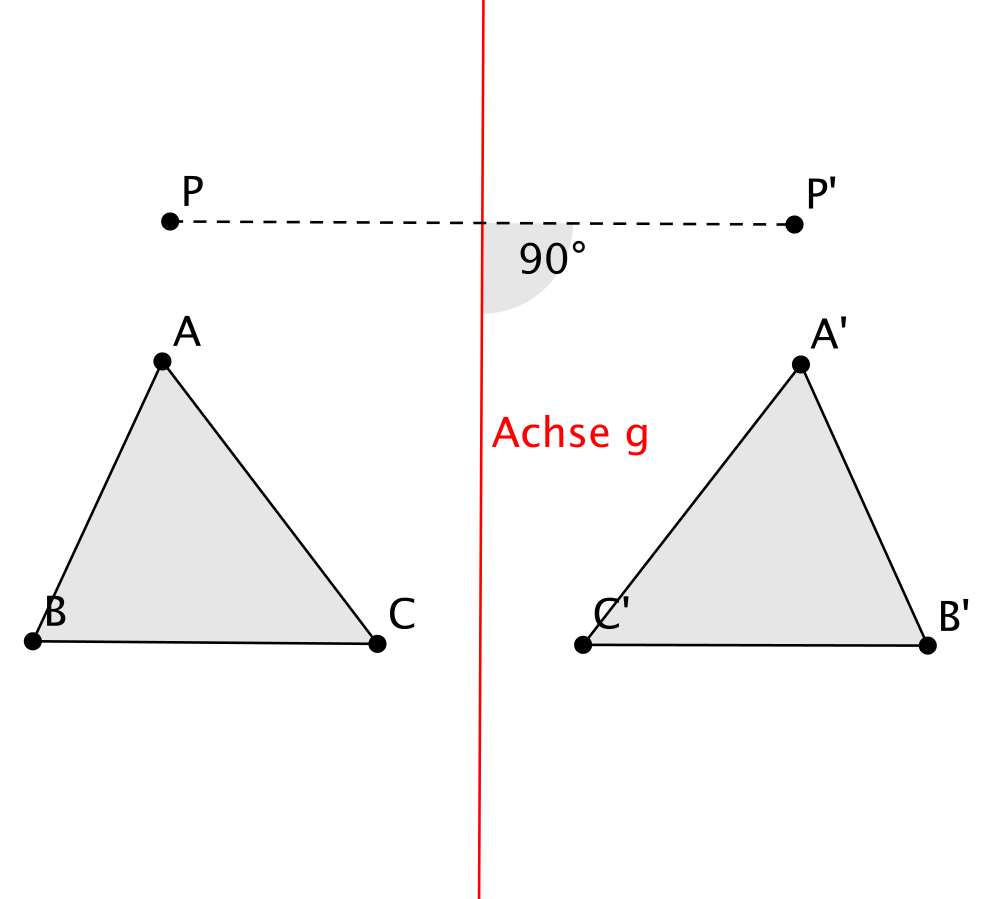Abb. 2.1.1

(2.2) Definition (Achsensymmetrie)

Eine ebene Figur \( F \) heißt achsensymmetrisch, wenn es eine Achsenspiegelung \( S_g \neq id \) gibt mit der Eigenschaft \( S_g(F) = F \), d. h. die Figur wird als Ganzes auf sich abgebildet.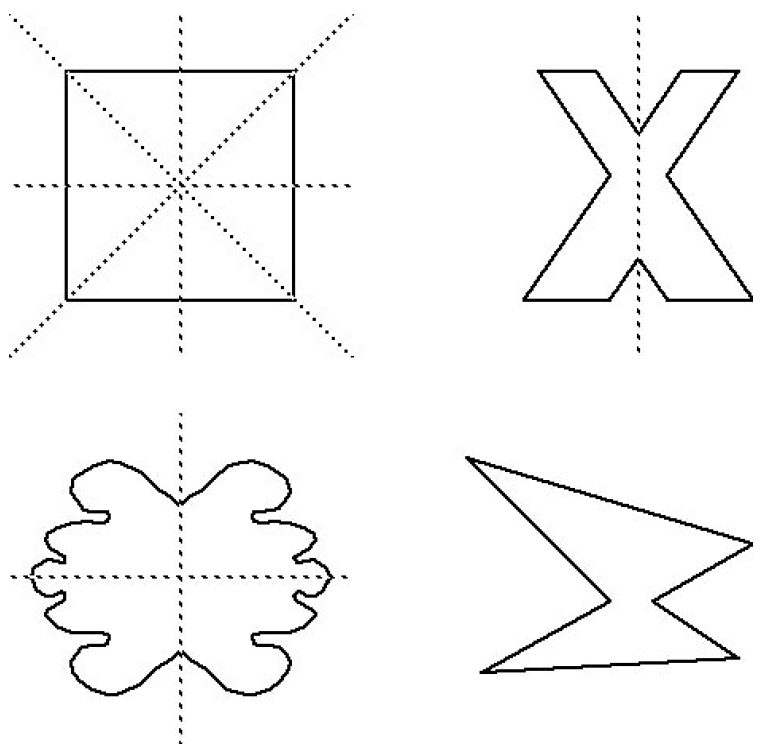

Abb. 2.1.2

2.2. Punktspiegelung & Punktsymmetrie

(2.3) Definition (Punktspiegelung)

Eine Abbildung \( S_z \) der Ebene auf sich heißt Punktpiegelung am Zentrum \( Z \), wenn für alle Punkte \( P \) gilt:

\( S_Z(Z) = Z \)
\( S_g(P) = P' \) für \( P \neq Z \) und \( Z \) Mittelpunkt von \( [PP'] \)

Abb. 2.2.1

(2.4) Definition (Punktsymmetrie)

Eine ebene Figur \( F \) heißt punktsymmetrisch, wenn es eine Achsenspiegelung \( S_Z \) gibt mit der Eigenschaft \( S_Z(F) = F \).

Abb. 2.2.2

2.3. Verschiebung & Verschiebungssymmetrie

(2.7) Definition (Verschiebung)

Eine Abbildung \( V_{h,r} \) der Ebene auf sich heißt Verschiebung in Richtung der Halbgeraden \( h \) um den Betrag \( r \in \mathbb{R}^{+}_{0} \), wenn für alle Punkte \( P \) gilt:

\( V_{h,r}(P) = P' \) mit \( PP'\ ||\ h \) und \( |PP'| = r \)

Abb. 2.3.1

(2.8) Definition (Verschiebungssymmetrie)

Eine ebene Figur \( F \) heißt verschiebungssymmetrisch, wenn es eine Verschiebung \( V_{h,r} \neq id \) gibt mit der Eigenschaft \( V_{h,r}(F) = F \).

Abb. 2.3.2

2.4. Drehung & Drehsymmetrie

(2.5) Definition (Drehung)

Eine Abbildung \( D_{Z,\alpha} \) der Ebene auf sich heißt Drehung um das Zentrum \( Z \) mit dem Winkel \( \alpha \), wenn für alle Punkte \( P \) gilt:

\( D_{Z,\alpha}(Z) = Z \)
\( D_{Z,\alpha}(P) = P' \) für \( P \neq Z \) mit \( |ZP| = |ZP'| \) und \( \measuredangle PZP' = \alpha \)

Abb. 2.4.1

(2.6) Definition (Drehsymmetrie)

Eine ebene Figur \( F \) heißt drehsymmetrisch, wenn es eine Drehung \( D_{Z,\alpha} \neq id \) gibt mit der Eigenschaft \( D_{Z,\alpha}(F) = F \).

Abb. 2.4.2

2.5. Kongruenz

Die verschiedenen Abbildungen (Achsenspiegelung, Punktspiegelung, Drehung und Verschiebung) sind längen- und winkelgetreu, d. h. dass sich die Form und Größe von beliebigen geometrischen Figuren nicht verändert. Dies führt zu einer Defintion von Kongruenz

(2.9) Definition (Kongruenzabbildung)

Eine längen- und winkelgetreue Abbildung der Ebene auf sich heißt Kongruenzabbildung. Eine ebene Figur heißt kongruent zu einer ebenen Figur \( F_2 \), wenn es eine Kongruenzabbildung \( \alpha \) gibt, so dass \( \alpha(F_1)=F_2 \).

Jede Art der Symmetrie lässt dich daher durch eine Bewegung (Kongruenzabbildung) erzeugen.

Kongruenzabbildung	in der Ebene	im Raum
Verschiebung \( t \)	um Vektor \( v \)	um Vektor \( v \)
Spiegelung \( s \)	an Gerade \( g \)	an Ebene \( E \)
Drehung \( d \)	um Punkt \( P \) mit Winkel \( \alpha \)	um Gerade \( g \) mit WInkel \( \phi \)
Gleitspiegelung \( t \circ s \) Schraubung \( t \circ d \) Drehspiegelung \( s \circ d \)	an Gerade \( g \), um Vektor \( v\ \|\|\ g \) -- --	an Ebene \( E \), um Vektor \( v\ \|\|\ E \) um Gerade \( g \), längs deren Richtungsvektor \( v \) um Gerade \( g \), an Ebene \( E \) mit \( E \perp g \)

Es ergeben sich daher Aussagen hinsichtlich Symmetrie und Kongruenz

(2.10) Folgerung

Symmetrie ist eine Eigenschaft geometrischer Figuren.
Kongruenz ist eine Relation zwischen Figuren.

3. Didaktischer Hintergrund

Symmetrie kann in jedem Alter Interesse wecken und zum eigenen Tun anregen. Die Möglichkeiten sind enorm: vom Klicksbild bis zur dreidimensionalen Computergrafik, vom Gleichgewichthalten bis zum Bestimmen von Eigenvektoren, von der intuitiven Wahrnehmung bei Mustern und Strukturen bis zur Defintion über die Invarianz gegenüber Kongruenzabbildungen. Der Begriff Symmetrie leitet sich vom griechischen symmetria für „Ebenmaß” ab. Ausgehend von handlungsorientierten Vorerfahrungen sollten auf Dauer zwei Arten der Definition vermittelt werden:

statische Definitionen über die gegenseitige Lage von Punkten, das Finden gleicher Strukturen
dynamisch motivierte Definitionen über die Invarianz gegenüber „Bewegungen”.

Der Übergang von physikalischen Bewegungen zu geometrischen Abbildungen ist mit einer Reihe didaktischer Schwierigkeiten verbunden. Diese sollten jedoch nicht davon abhalten, Bewegungen als Grunderfahrungen in die Symmetriebehandlung mit einzubezihen. Lebendiges Wissen über Symmetrieorgane (Spiegelpunkte, -geraden und -ebenen, Drehzentren und Drehwinkel), Invarianten und Eigenschaften von „Bewegungen” (Fixpunkte, Fixgeraden und Fixebenen, Längen-, Verhältnis- und Winkeltreue, ggf. Orientierungsänderung) sowie deren Verkettung und Inversion geben als Fernziel eine sinnvolle Richtung vor.

Der Symmetriebegriff braucht tragfähige Grunderfahrungen (blauer Kasten) – um ihrer selbst Willen, als Fundament für spätere inner- und außermathematische Erfahrungen, als Mittel der Umwelterschließung und als Kulturtechnik. Solche Erfahrungen werden zum Teil bereits vor und in der Grundschule gesammelt, sollten aber wach gehalten und ausgebaut werden. Sie sollten die Analyse und Synthese symmetrischer Figuren gleichermaßen berücksichtigen und auch die Fragen mit einschließen, infolge welcher Entstehungsbedingungen oder mit welchem zweck Objekte symmetrisch sind.

Auswahl wichtiger (Grund-)Erfahrungen zum Symmetriebegriff

sich Bewegen (Gleichgewicht)
Ertasten (symmetrische Flächen und Körper)
Falten (Klecksbilder, Origami)
Sortieren (von Objekten nach Symmetrieeigenschaften)
Erzeugen symmetrischer Formen (Geobrett, Mandalas)
Symmetrieorgane zeichnen (Spieglachsen und -Punkte, Drehzentren, Verschiebungspfeile)

Die folgenden sechs Beispiele zeigen, warum sich der Erwerb von Symmetriekenntnissen schon rein innermathematisch lohnt und inwiefern er in Verbindung mit anderen wichtigen Lehrplaninhalten erfolgen kann.

Symmetrie als kreatives Mittel:
Symmetrie wird als ästhetisch empfunden und spricht an. Manchmal machen auch gerade die (kleinen) Symmetriebrüche den Reiz einer Sache aus. Und je größer die Kenntnisse und Fertigkeiten, desto größer die kreativen Möglichkeiten, vom Zeichnen einfacher geometrischer Formen bis zum (Er-)finden von Mustern in komplexeren Strukturen wie Mandala.

Symmetrie als Ordnungsmerkmal:

Einen nahe liegenden Einstieg in das Thema Symmetrie bietet das Sortieren der beteiligten Buchstaben nach ihren Symmetrieigenschaften. Auch die übrigen Buchstaben und Ziffern, Zeichen und geometrische Objekt aller Art können nach Symmetriekriterien geordnet werden. Das Ausmaß von Symmetrien (die Ordnung der Symmetriegruppe) bringt Struktur in die Geometrie.

Symmetrie als Hilfe beim Problemlösen:

Mathematiker arbeiten gerne elegant und effektiv. Dabei können Symmetrieeingenschaften eine große Hilfe sein, sofern man sie bemerkt und nutzt. Oberstufenschüler kennen dies vor allem von der Kurvendiskussion: Kann man anhand des Funktionsterms nachweisen, dass der Graph symmetrisch zur y-Achse oder zum Ursprung ist, genügt ab dann die Unteruschung des positiven Bereichs. In der Geometrie können Symmetrieiegenschaften von Figuren und Körpern zur Berechnung von Längen, Flächeninhalten und Volumina genutzt werden. Darüber hinaus können symmetrische Anordnungen eine erhebliche Hilfe bei Abzählproblemen sein.

Weitere Beispiele sind gegeben durch:

Symmetrie als Nebeneffekt
Symmetrie als Ziel
Symmetrie als optimaler Fall
Symmetrisieren als heuristische Strategie

In den Bildsungsstandards für den mittleren Schulabschluss in Mathematik von 2003 findet man den Begrff Symmetrie explizit nur unter den Lernzielen zu Raum und Form (vgl. [QUELLE], S. XX). Konkret sind in allen Bundesländern ebene Achsen- und Punktsymmetrie obligatorisch. In diesem Kontext erwartete Kompetenzen sind etwa:

grundlegende Symmetrien mit angemessenen Fachausdrücken beschreiben
symmetrische Objekte identifizieren
symmetrische Figuren erzeugen / Symmetrie als Gestaltungsobjekt nutzen
mit Symmetrie Größen berechen und Figureneigenschaften begründen
Spiegelpunkte, Spiegelachsen und Drehzentren konstruieren.

Für die Einführung von Symmetrie und Kongruenz im Mathematikunterricht ergeben sich durch den Zusammenhang von Symmetrie und Kongruenz zwei verschiedene Möglichkeiten. Entweder kann über die Symmetrie zum Begriff der Kongruenz herangeführt werden oder entsprechend umgekehrt von der Kongruenz zum Begriff der Symmetrie.

Symmetrie → Kongruenz:

Für den ersten Zugang zum Begriff der Symmetrie sind die jeweiligen vier Abbildungen zur Achsenspiegelung, Punktspiegelung, Drehung und Verschiebung anzugeben. Eine jeweilige symmetrische Figur ist gegenüber der jeweiligen Abbildung invariant. Mit Hilfe der Abbildungen können Figur und Bidfigur miteinander in Deckung gebracht werden und sind somit kongruent. Es entsteht folglich die Überleitung zum Begriff der Kongruenzabbildung.
Für die Kongruenz von Figuren ergibt sich insgesamt

Zwei Figuren sind kongruent oder deckungsgleiech, wenn man sie durch Achsenspiegelung, Verschiebung oder eine Kombination aus beiden zur Deckung bringen kann.

Kongruenz → Symmetrie:

Wird zuerst der Begriff der Kongruenz beispielsweise über Kongruenzsätze im Dreieck (SSS, SWS, WSW, SsW) eingeführt, kann eine Überleitung zur Symmetrie beispielsweise gegeben werden durch

Eine Figur heißt achsensymmetrisch, wenn man sie durch eine Gerade g in zwei zueinander kongruente Teilfiguren unterschiedlicher Orientierung zerlegen kann. (vgl. Abb 3.1)

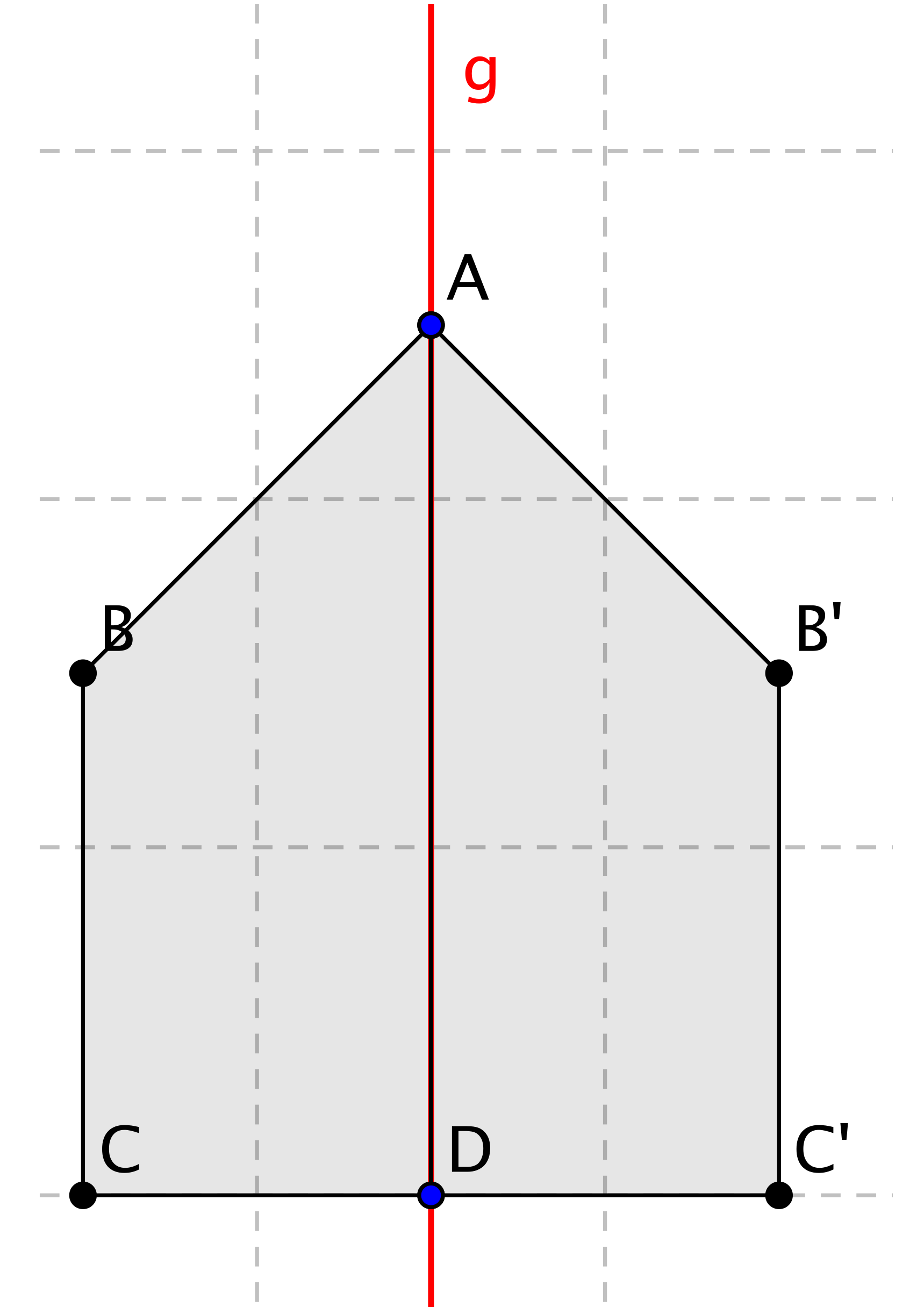
Bild zur Achsensymmetrie über Kongruenzbegriff

Abb. 3.1: Symmetrie über Kongruenzbegriff

4. Unterrichtsbaustein

Da im Rahmen des nun beschlossenen Digitalpakts Schule durch die Bundesregierung fünf Milliarden Euro zur Förderung der Digitalisierung bereitstehen, wird die Verfügbarkeit von technischen Geräten in Schulen künftig steigen. In Anlehnung an diese Vorgänge ist es notwendig, dass auch auf Seiten der Lehrkräfte die Konzeption oder Nutzung von digitalen Angeboten intensiviert wird. Eine Möglichkeit zur Nutzung von digitalen Bildungsinhalten bietet die unter GNU-Lizenz veröffentlichte Software GeoGebra. Im Folgenden werden zwei GeoGebra-Aktivitäten vorgestellt, die für einen exemplarischen Unterrichtsbaustein verwendet werden könnten. Die jeweilige konkrete Nutzung der Aktivität hängt aber immer von den vorhandenen technischen Geräten ab. Verfügen die SuS nicht über eigene Gerätschaften im Mathematikunterricht, so kann eine Nutzung der Aktivitäten nur in einem zentralen Unterrichtsgespräch stattfinden.

Erster Baustein: Symmetrie von Verkehrsschildern

Nach der Einführung von Symmetrieachsen kann mit Hilfe der GeoGebra-Aktivität eine alltagszugewandte Komponente eingeführt werden. Verkehrsschilder begegnen den SuS jeden Tag und sind auch (zumindest Grundzeichen wie Vorfahrt oder Stopp) in ihrer Bedeutung bekannt. Dadurch kann gegenüber den SuS verdeutlicht werden, wie stark Symmetrie auch im Alltag vertreten ist. Die Aktivität kann gezielt zur Sicherung und Überprüfung des Wissen bezüglich des Verständnisses von Symmetrieachsen genutzt werden und steht somit als Baustein am Ende einer Unterrichtssequenz.

1. GeoGebra-Aktivität:
Die Aktivität kann sowohl im Rahmen eines Unterrichtsgesprächs als auch im Rahmen einer Einzelarbeit der SuS genutzt werden. Nutzung: Die jeweiligen Verkehrsschilder sind gemäß ihres Aussehens in die Boxen symmetrisch oder nicht symmetrisch zu ziehen. Bei korrekter Zuordnung erscheint ein Smiley.

2. Finden weiterer symmetrischer Gegenstände:
Finde und fotografiere (oder suche und speichere Fotos von) Gegenstände/Vorgänge aus dem Alltag (keine Marken oder Personen!), die symmetrisch gebaut/gestaltet/gemalt (etc.) sind. Zeichne im Anschluss eine mögliche Symmetrieachse ein.

Didaktische Einordnung:
Die eher offene Aufgabenstellung der zweiten Aufgabe ermutigt die SuS dazu selbst aktiv zu werden. Dadurch das Symmetrie nicht beschränkt ist auf einen Interessenbereich, sondern sich durch die Technik-, Tier- und Sportwelt zieht, sind die SuS nicht inhaltlich beschränkt und können auch im Rahmen ihrer eigenen Interessen nach symmetrischen Gegenständen/Vorgängen suchen. Die zweite Aufgabe könnte vor allem als offene Hausaufgabe mit auf den Weg gegeben werden. Zum einen kann aufgrund der technischen Möglichkeiten durch die jeweiligen Geräte schnell ein Foto gemacht werden, zum anderen ist eine Übertragung (z. B. in einen Moodle-Lernraum) denkbar, sodass die Bilder und Fotos zu Beginn der nächsten Unterrichtsstunde zentral angezeigt werden können per Beamer/Whiteboard. Eine solche Aufgabe für außerhalb des Unterrichts kann als eher unproblematisch angesehen werden, da bereits im Alter von 13 Jahren eine fast vollständige Versorgung mit privaten digitalen Endgeräten auf Seiten der SuS vorhanden ist (vgl. [3], S. 25).
In didaktischer Hinsicht werden durch den Unterrichtsbaustein vor allem die prozessbezogenen Kompetenzen Modellieren und Werkzeuge nutzen angesprochen. Die SuS übersetzen in beiden Aufgaben jeweils eine Realsituation in ein mathematisches Modell und erheben durch die Fotos und Bilder darüber hinaus eigene Daten. Darüber hinaus werden durch die Nutzung von GeoGebra und Smartphone die angemessene Nutzung gefördert. Weiterhin befinden sich beide Aufgabenteile auch zwangsläufig im Prozessbereich Argumentieren/Kommunizieren, da durch die SuS die Zuordnung der Verkehrsschilder begründet werden muss und auch bei der zweiten Aufgabe eine Begründung angegeben werden muss, wieso das vorgestellte Motiv symmetrisch ist und wo sich die Symmetrieachse befindet. Darüber hinaus besteht in der zweiten Aufgabe zumindest die eingeschränkte Möglichkeit einen ekativen Teil zu ermöglichen. Gegenstände wie (Fuß-)bälle oder auch Tiere können in der Regel angefasst werden, sodass eine weitere Ebene der Wahrnehmung vorhanden sein kann. Für Fotos gilt dies aber entsprechend nicht.

Zweiter Baustein: Kongruenz bei Verschiebung und Drehung

Die Visualisierung von Kongruenzabbildungen stellt die Lehrkaft bei der Nutzung von Tafel und Kreide vor mehrere Probleme. Das Zeichnen an der Tafel ist zeitraubend und es lässt sich immer nur ein konkretes Beispiel zeichnen. Mit Hilfe einer Visualisierung können die SuS selbst die jeweiligen Kongruenzabbildungen entdecken. Durch die Möglichkeit der manuellen Änderung entfällt zudem die Beschränkung der dargestellten Versionen an der Tafel. Nach der Einführung von Verschiebung und Drehung kann die Aktivität genutzt werden, um möglichen Fehlvorstellungen vorzubeugen, dass die Drehung und Verschiebung auf einzelne Dreiecke beschränkt ist, obwohl jedes Dreieck verschoben und gedreht werden kann. Darüber hinaus kann durch die manuelle Veränderung des Dreiecks sofort die Änderung der Verschiebung und Drehung beobachtet werden ohne das eine neue aufwendige Zeichnung nötig ist. Der Unterrichtsbaustein sollte nach der Vermittlung des Inhalts (Einführung und Konstruktion von Verschiebung und Drehung) angesetzt werden.

1. GeoGebra-Aktivität:
Die Aktivität kann ebenfalls sowohl im Rahmen eines Unterrichtsgesprächs als auch im Rahmen einer Einzelarbeit der SuS genutzt werden. Entsprechend des Wissenstands kann auch nur die Verschiebung oder nur die Drehung betrachtet werden. Nutzung: Durch das Ziehen des blauen Dreiecks kann nach der entsprechenden Auswahl links die Drehung und Verschiebung des Dreiecks betrachtet werden.

Um der Annahme vorzubeugen, dass nur Dreiecke verschoben und gedreht werden können, ist es möglich weitere Figuren hinzuzuiehen. In der folgenden Aufgabe wird daher der Buchstabe F entsprechend (der Halbgeraden) verschoben und gedreht.

2. Eigene Verschiebung und/oder Drehung:

Verschiebe den gegebenen Buchstaben auf dem Blatt entsprechend des bereits über die Halbegrade verschobenen Punkts \( A \) zu \( A' \). Drehe im Anschluss den Buchstaben um \( 60° \) um das gegebene Drehzentrum \( Z \).

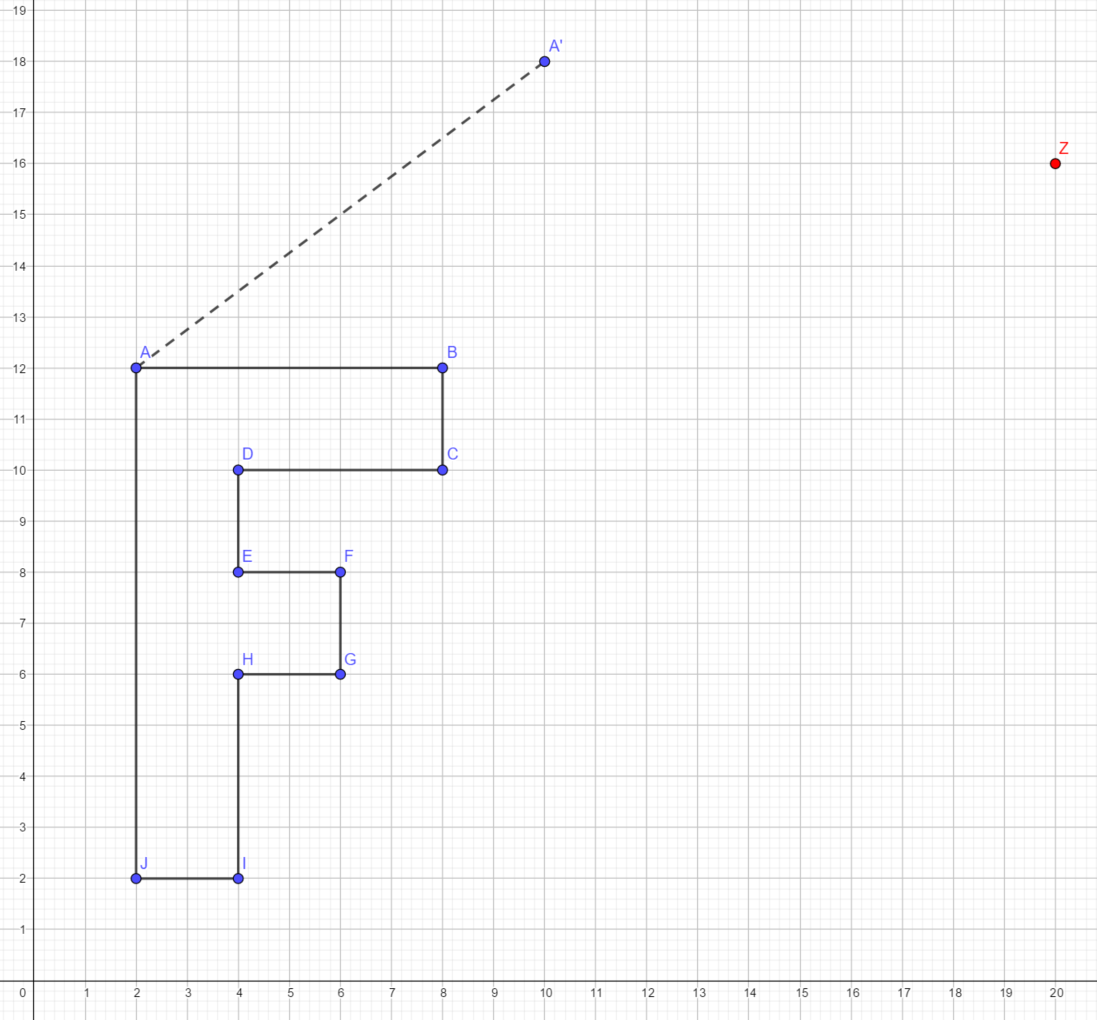Bild des Buchstabens F zur Verschiebung und Drehung

Abb. 4.1: Buchstabe F bestehend aus den gegebenen Punkten, die Halbgerade und das Drehzentrum \( Z \).

(Hier ist die Ausgabe eines entsprechenden Arbeitsblatts erforderlich. Alternativ kann auch hier ein vorhandes digitales Gerät zusammen mit GeoGebra genutzt werden. Da bei Prüfungen jedoch auch auf Papier gezeichnet werden muss, ist hier eine Einschränkung der digitalen Geräte möglich.)

Didaktische Einordnung:

Die SuS können verschiedene Verschiebungen und Drehungen über die GeoGebra-Aktivität direkt einsehen und sind nicht auf einzelne Tafelbeispiele beschränkt. Die visuelle Komponente wird also bewusst gestärkt. Die eigene Anwendung des vorher vermittelnden Inhalts ist jedoch notwendig, um auch eine sichere Beherrschung mit Stift und Papier sicherzustellen (auch im Hinklick auf formale Fertigkeiten). In der zweiten Aufgabe ist daher der Prozessbereich Werkzeuge nutzen von Bedeutung. Zur Verschiebung und Drehung des Buchstaben ist die genaue Nutzung eines Geodreiecks notwendig.

5. Fazit & Reflexion

In der Mathematik gibt es neben symmetrischen Flächen und Körpern auch symmetrische Relationen, symmetrische Gruppen, symmetrische Matrizen und symmetrische Operatoren und sie alle haben innerhalb ihres Bereichs besondere Bedeutung. Tragfähige Symmetrierfahrungen bilden die Basis für weiterführende mathematische und naturwissenschaftiche Themen. In der Oberstufe betrifft dies vor allem die Behandlung von Matrizen als Repräsentanten Linearer Abbildungen. Im Studium betrifft es beispielsweise die Gruppen- und Galoistheorie oder auch die komplexen Zahlen.

Das Thema Symmetrie kann als überdurchschnittlich allgemeinbildend und attraktiv beschrieben werden. Durch die Symmetrie können exemplarisch wichtige Charakteristika der Wissenschaft Mathematik vermittelt werden.

6. Literatur

Allgemeine Literatur:

Weigand, H.-G. et al.(Hrsg.)(2009): Didaktik der Geometrie für die Sekundarstufe I..Kap.VI I I. Symmetrie und Kongruenz von Schmidt-Thieme, B./Weigand, H.-G., S.187-215.
Der Abschnitt behandelt das Thema der Symmetrie und Kongruenz. Dabei werden zunächst Mathematische Grundlagen von Symmetrie und Kongruenz dargestellt, die als fachlicher Hintergrund wichtig sind. Danach wird Symmetrie als Umweltphänomen vorgestellt und einige Beispiele gegeben. Anschließend wird das Lernen des Symmetriebegriffs behandelt, was den didaktischen Hintergrund präsentiert und auch das in meiner Ausarbeitung behandelte Stufenlernsystem thematisiert. Folglich werden Beispiele und Anwendungen des Symmetriebegriffs zu Beginn der Sekundarstufe 1 veranschaulicht. Zuletzt wird die Kongruenz nochmal genauer betrachtet und Symmetrien und Kongruenzen im Raum behandelt.
Heitzer, J. (2010): Symmetrie im Mathematikunterricht. In: mathematik lehren 161, S. 4-11. Velber: Friedrich Verlag. Der Abschnitt thematisiert die Symmetrie im Mathematikunterricht. Die Symmetrie wird in Bezug zum Kernlehrplan gesetzt und methodisch, inhaltlich und fachdidaktisch gut durchleuchtet. Dazu werden sehr gute Einstiegsmöglichkeiten in den Unterricht bzw. das Thema Symmetrie dargestellt, beispielsweise das Anknüpfen an Vorerfahrungen, die die SchülerInnen schon mitbringen. Des Weiteren wird einem nahe gebracht, warum es sich überhaupt lohnt Symmetrien zu kennen, womit die Sinn-Frage beantwortet wäre und Symmetrien nicht nur in der Geometrie thematisiert werden und bedeutend sind. Zuletzt werden noch einige Aufgaben zur Symmetrie vorgestellt.
Kinder-Medien-Studie (2018): Kinder-Medien-Studie 2018. URL: https://kinder-medien-studie.de/wp-content/uploads/2018/08/KMS_Handout_PK2018_FINAL_V2.pdf
Quelle für Information zur Austattung mit digitalen Endgeräten von Kindern und Jugendlichen.
Weyl, H. (1955): Symmetrie. Birkhäuser Verlag, Basel.
Zitat für die Einleitung.

Bildnachweise:

Pflanzenblatt, Autor: klickblick (Pixabay License), Link: https://pixabay.com/de/photos/natur-pflanze-blatt-gegenlicht-3412504/
Hausfront, Autor: Free-Photos (Pixabay License), Link: https://pixabay.com/de/photos/architektur-geb%C3%A4ude-symmetrie-864367/
Flugzeug, Autor: PublicDomainPictures (Pixabay License), Link: https://pixabay.com/de/photos/passagierflugzeug-passagier-jet-19469/
Abb. 2.1.1: Autor: Dziatzko, S. (2015). In: Symmetrie und Kongruenz. Vortrag zum Seminar Mathematik präsentieren und vermitteln.
Abb. 2.1.2: Autor: Loggie (Public Domain), Link: https://commons.wikimedia.org/wiki/File:Symmetry.jpg
Abb. 2.2.1: Autor: Dziatzko, S. (2015). In: Symmetrie und Kongruenz. Vortrag zum Seminar Mathematik präsentieren und vermitteln.
Abb. 2.2.2: Link: https://www.plakos.de/fileadmin/test/punktsymmetrie-buchstabe-N.png
Abb. 2.3.1: Autor: Dziatzko, S. (2015). In: Symmetrie und Kongruenz. Vortrag zum Seminar Mathematik präsentieren und vermitteln.
Abb. 2.3.2: Link: http://www.blikk.it/angebote/primarmathe/bilder/ma2640b.gif
Abb. 2.4.1: Autor: Dziatzko, S. (2015). In: Symmetrie und Kongruenz. Vortrag zum Seminar Mathematik präsentieren und vermitteln.
Abb. 2.4.2: Autor: kmicican (Pixabay License), Link: https://pixabay.com/vectors/ornament-highlander-highlanders-2009339/
Abb. 3.1: Autor: Dziatzko, S. (2015). In: Symmetrie und Kongruenz. Vortrag zum Seminar Mathematik präsentieren und vermitteln.
Abb. 4.1: Eigenes Werk.

Site:	RWTHmoodle
Course:	Grundlagenwissen Mathematikdidaktik
Book:	Symmetrie und Kongruenz

Printed by:	, Guest user
Date:	Monday, 20 May 2024, 2:01 PM