Symmetrie kann in jedem Alter Interesse wecken und zum eigenen Tun anregen. Die Möglichkeiten sind enorm: vom Klicksbild bis zur dreidimensionalen Computergrafik, vom Gleichgewichthalten bis zum Bestimmen von Eigenvektoren, von der intuitiven Wahrnehmung
bei Mustern und Strukturen bis zur Defintion über die Invarianz gegenüber Kongruenzabbildungen. Der Begriff Symmetrie leitet sich vom griechischen symmetria für „Ebenmaß” ab. Ausgehend von handlungsorientierten Vorerfahrungen sollten auf Dauer
zwei Arten der Definition vermittelt werden:
- statische Definitionen über die gegenseitige Lage von Punkten, das Finden gleicher Strukturen
- dynamisch motivierte Definitionen über die Invarianz gegenüber „Bewegungen”.
Der Übergang von physikalischen Bewegungen zu geometrischen Abbildungen ist mit einer Reihe didaktischer Schwierigkeiten verbunden. Diese sollten jedoch nicht davon abhalten, Bewegungen als Grunderfahrungen in die Symmetriebehandlung mit
einzubezihen. Lebendiges Wissen über Symmetrieorgane (Spiegelpunkte, -geraden und -ebenen, Drehzentren und Drehwinkel), Invarianten und Eigenschaften von „Bewegungen” (Fixpunkte, Fixgeraden und Fixebenen, Längen-, Verhältnis- und Winkeltreue, ggf.
Orientierungsänderung) sowie deren Verkettung und Inversion geben als Fernziel eine sinnvolle Richtung vor.
Der Symmetriebegriff braucht tragfähige Grunderfahrungen (blauer Kasten) – um ihrer selbst Willen, als Fundament für spätere inner- und außermathematische Erfahrungen, als Mittel der Umwelterschließung und als Kulturtechnik. Solche Erfahrungen werden
zum Teil bereits vor und in der Grundschule gesammelt, sollten aber wach gehalten und ausgebaut werden. Sie sollten die Analyse und Synthese symmetrischer Figuren gleichermaßen berücksichtigen und auch die Fragen mit einschließen, infolge
welcher Entstehungsbedingungen oder mit welchem zweck Objekte symmetrisch sind.
|
Auswahl wichtiger (Grund-)Erfahrungen zum Symmetriebegriff
|
-
sich Bewegen (Gleichgewicht)
- Ertasten (symmetrische Flächen und Körper)
- Falten (Klecksbilder, Origami)
- Sortieren (von Objekten nach Symmetrieeigenschaften)
- Erzeugen symmetrischer Formen (Geobrett, Mandalas)
- Symmetrieorgane zeichnen (Spieglachsen und -Punkte, Drehzentren, Verschiebungspfeile)
|
Die folgenden sechs Beispiele zeigen, warum sich der Erwerb von Symmetriekenntnissen schon rein innermathematisch lohnt und inwiefern er in Verbindung mit anderen wichtigen Lehrplaninhalten erfolgen kann.
Symmetrie als kreatives Mittel:
Symmetrie wird als ästhetisch empfunden und spricht an. Manchmal machen auch gerade die (kleinen) Symmetriebrüche den Reiz einer Sache aus. Und je größer die Kenntnisse und Fertigkeiten, desto größer die kreativen
Möglichkeiten, vom Zeichnen einfacher geometrischer Formen bis zum (Er-)finden von Mustern in komplexeren Strukturen wie Mandala.
Symmetrie als Ordnungsmerkmal:
Einen nahe liegenden Einstieg in das Thema Symmetrie bietet das Sortieren der beteiligten Buchstaben nach ihren Symmetrieigenschaften. Auch die übrigen Buchstaben und Ziffern, Zeichen und geometrische Objekt aller Art können nach Symmetriekriterien
geordnet werden. Das Ausmaß von Symmetrien (die Ordnung der Symmetriegruppe) bringt Struktur in die Geometrie.
Symmetrie als Hilfe beim Problemlösen:
Mathematiker arbeiten gerne elegant und effektiv. Dabei können Symmetrieeingenschaften eine große Hilfe sein, sofern man sie bemerkt und nutzt. Oberstufenschüler kennen dies vor allem von der Kurvendiskussion: Kann man anhand des Funktionsterms nachweisen,
dass der Graph symmetrisch zur y-Achse oder zum Ursprung ist, genügt ab dann die Unteruschung des positiven Bereichs. In der Geometrie können Symmetrieiegenschaften von Figuren und Körpern zur Berechnung von Längen, Flächeninhalten und Volumina genutzt
werden. Darüber hinaus können symmetrische Anordnungen eine erhebliche Hilfe bei Abzählproblemen sein.
Weitere Beispiele sind gegeben durch:
- Symmetrie als Nebeneffekt
- Symmetrie als Ziel
- Symmetrie als optimaler Fall
- Symmetrisieren als heuristische Strategie
In den Bildsungsstandards für den mittleren Schulabschluss in Mathematik von 2003 findet man den Begrff Symmetrie explizit nur unter den Lernzielen zu Raum und Form (vgl. [QUELLE], S. XX). Konkret sind in allen Bundesländern ebene Achsen- und Punktsymmetrie
obligatorisch. In diesem Kontext erwartete Kompetenzen sind etwa:
- grundlegende Symmetrien mit angemessenen Fachausdrücken beschreiben
- symmetrische Objekte identifizieren
- symmetrische Figuren erzeugen / Symmetrie als Gestaltungsobjekt nutzen
- mit Symmetrie Größen berechen und Figureneigenschaften begründen
- Spiegelpunkte, Spiegelachsen und Drehzentren konstruieren.
Für die Einführung von Symmetrie und Kongruenz im Mathematikunterricht ergeben sich durch den Zusammenhang von Symmetrie und Kongruenz zwei verschiedene Möglichkeiten. Entweder kann über die Symmetrie zum Begriff der Kongruenz herangeführt werden
oder entsprechend umgekehrt von der Kongruenz zum Begriff der Symmetrie.
Symmetrie → Kongruenz:
Für den ersten Zugang zum Begriff der Symmetrie sind die jeweiligen vier Abbildungen zur Achsenspiegelung, Punktspiegelung, Drehung und Verschiebung anzugeben. Eine jeweilige symmetrische Figur ist gegenüber der jeweiligen Abbildung invariant.
Mit Hilfe der Abbildungen können Figur und Bidfigur miteinander in Deckung gebracht werden und sind somit kongruent. Es entsteht folglich die Überleitung zum Begriff der Kongruenzabbildung.
Für die Kongruenz von Figuren ergibt
sich insgesamt
Zwei Figuren sind kongruent oder deckungsgleiech, wenn man sie durch Achsenspiegelung, Verschiebung oder eine Kombination aus beiden zur Deckung bringen kann.
Kongruenz → Symmetrie:
Wird zuerst der Begriff der Kongruenz beispielsweise über Kongruenzsätze im Dreieck (SSS, SWS, WSW, SsW) eingeführt, kann eine Überleitung zur Symmetrie beispielsweise gegeben werden durch
Eine Figur heißt achsensymmetrisch, wenn man sie durch eine Gerade g in zwei zueinander kongruente Teilfiguren unterschiedlicher Orientierung zerlegen kann. (vgl. Abb 3.1)
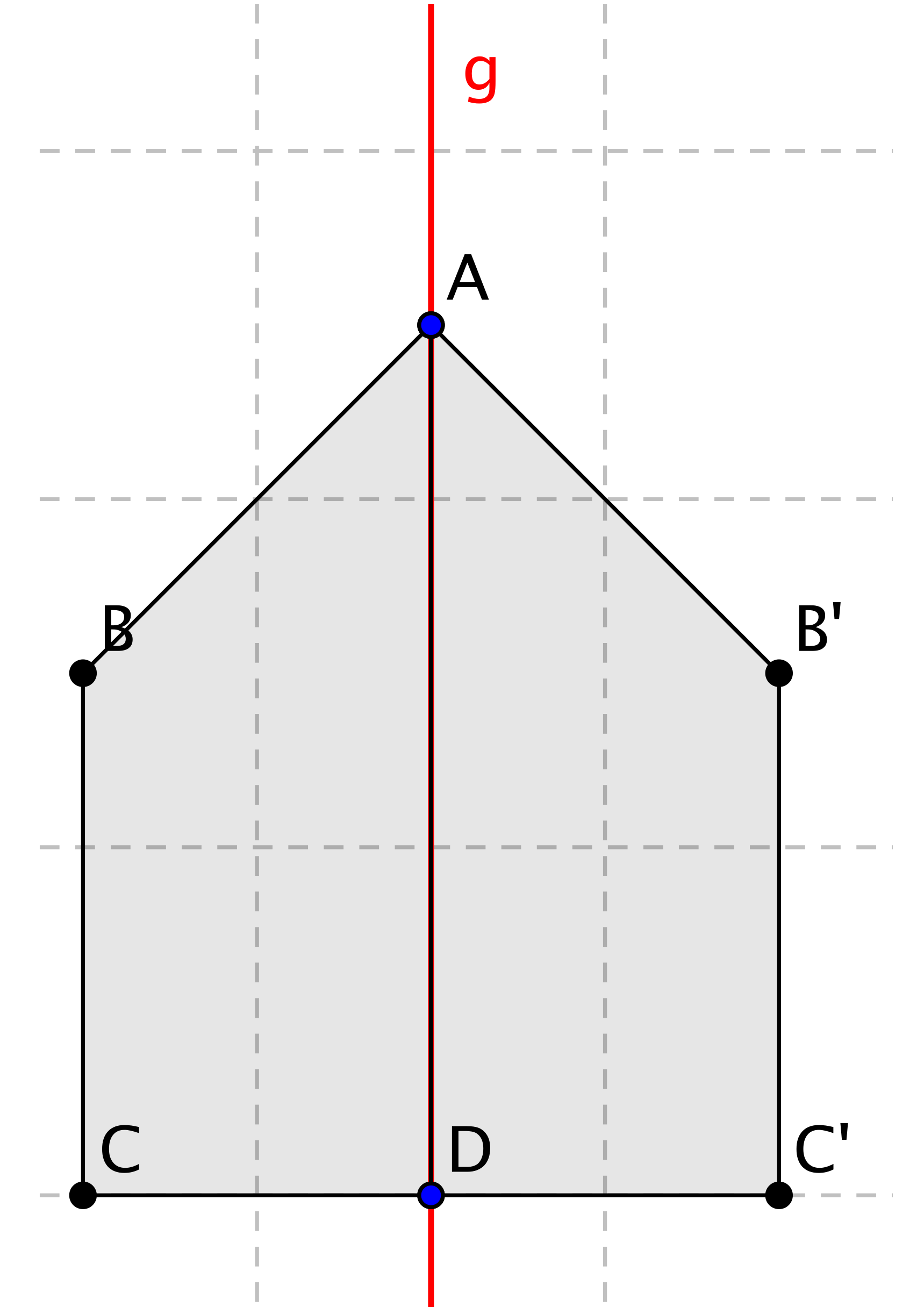
Abb.
3.1: Symmetrie über Kongruenzbegriff

 RWTHmoodle-Hilfe
RWTHmoodle-Hilfe
 +49 241 / 80-24680
+49 241 / 80-24680 +49 241 / 80-22981
+49 241 / 80-22981

